Постановка проблемы. В настоящее время в большинстве действующих программ для детского сада оригами позиционируется как одно из средств конструирования, обладающее потенциалом для развития когнитивной сферы.
Оригами (яп. “ори” – сложить, “ками” – бумага) – складывание из бумаги. Сходство звучания японских слов “бумага” и “бог” – “Ками” породило мистическую связь между религиозными ритуалами и изделиями из сложенной бумаги. С 1185 г. владение оригами стало необходимым требованиям японского дворцового этикета, признаком хорошего образования. Знатные семьи использовали фигурки оригами как герб и печать. С 1600 г. оригами из церемониального искусства стало превращаться в любимое хобби [1].
Со второй половины XIX в. европейцы получили возможность познакомиться с японским оригами. До того искусством складывания в Европе занимались мало, за исключением Фридриха Фребеля, который одним из первых начал пропагандировать складывание из бумаги как дидактический метод для объяснения детям простых правил геометрии.
После Второй мировой войны всемирно признанный японский мастер Акира Йошизава изобрел несложные условные знаки, благодаря чему процесс складывания любого изделия оригами оказалось возможным представить в виде серии рисунков-чертежей.
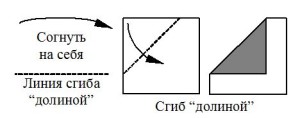
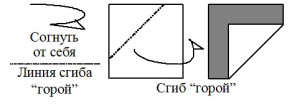
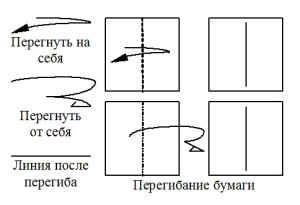
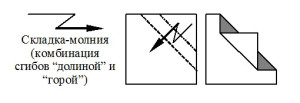
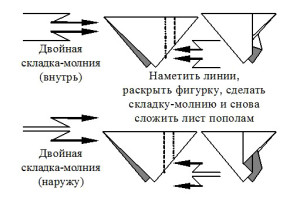
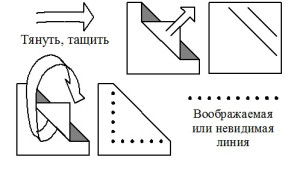
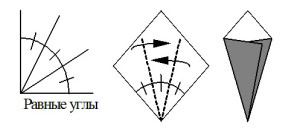
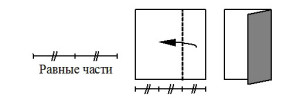
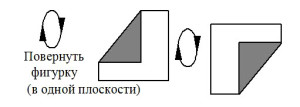
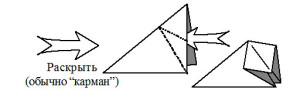
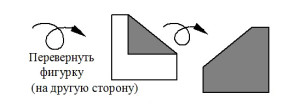
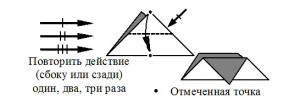
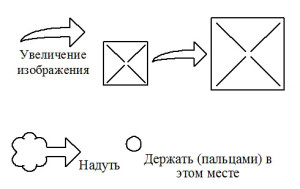
Наиболее часто используемые условные знаки оригами приведены на рис. 1. Согласно нашим наблюдениям, все эти знаки доступны детям 6-7 лет для оперирования в ходе группового и индивидуального моделирования на материале оригами.
Рисунок 1. Основные международные условные обозначения оригами
Важная особенность оригами, способствовавшая его быстрому распространению, – неограниченные комбинаторные возможности, кроющиеся в обычном листе бумаги. С точки зрения элементарной математики, исходная фигура f (базовая форма) переходит в фигуру f1 (готовая модель) без разрывов и склеиваний, то есть происходит гомеоморфное отображение f в f1 (греч. “гомео” – подобный, “морфе” – форма). Свойства фигур, которые сохраняются при гомеоморфных отображениях, называют топологическими, поэтому, с позиций математического моделирования, уместно говорить о топологическом моделировании на материале базовых форм и модулей оригами. Действительно, при грамотном методическом сопровождении процесса складывания, дети обогащают математический словарь и приобретают представления об осевой симметрии, подобии, движении фигур, являющихся частными случаями топологических преобразований.
Анализ исследований и публикаций. Полезно придерживаться следующих технологических правил, сформулированных на основе анализа исследований С.Ю. Афонькина, Е.Ю. Афонькиной, С.Н. Белим, И.В. Капитоновой, О.С. Кузнецовой, Т.Ю. Погребняк, Н.А. Простяковой, В.П. Чернова и других исследователей.
Начинайте моделирование с простейших фигур, вид которых не слишком абстрактен. Во время занятия актуализируйте имеющиеся у детей знания об окружающем мире, расширяйте их. Демонстрируйте складывание с помощью большого квадрата, с одной стороны белого, с другой – цветного.
На первых занятиях демонстрируйте процесс складывания без схем, используя сказочный сюжет (логичный или парадоксальный). Постепенно приучайте ребят к условным знакам (рис. 1), схемам. Правильно используйте математические термины, используемые при моделировании (точка, отрезок, угол, треугольник, квадрат, прямоугольник, ромб, параллельные прямые, равные отрезки, равные углы, равные фигуры, подобные треугольники, прямой угол, острый угол, тупой угол, биссектриса угла, сторона, середина стороны, средняя линия, ось симметрии, диагональ и др.).
Просите ребят складывать дома для папы и мамы те фигурки, которые они научились делать в саду. После того как дети научились моделировать пять-шесть фигурок – организуйте конкурс “юных оригамистов” по двум номинациям: кто быстрее и кто качественнее смоделирует фигурку. Собирайте новые фигурки, сложенные детьми самостоятельно, фиксируйте авторство детей.
Логика построения занятия: репродуктивное моделирование – самостоятельное моделирование – творческое моделирование. Возможные типы заданий: сложить модель по памяти; сложить модель по схеме; сложить модель по словесному руководству; разобрать готовую модель и зарисовать схему ее моделирования; создать новую модель [3].
Результаты исследований. Нами была разработана и апробирована серия занятий по топологическому моделированию: пять занятий на основе простейших классических базовых форм оригами и 7 занятий на основе моделей оригами “Звездное небо” Т.В. Хлямовой [4] и материалов Н.В. Нищевой [2]. Занятия успешно апробированы в 2008–2009 уч. г. на базе прогимназии “Полянка” г. Смоленска (директор И.Ю. Новикова, зам. директора Е.В. Васильева).
Занятия на основе базовых форм оригами включали знакомство с условными знаками оригами (рис. 1), со схемами моделирования выбранных базовых форм (рис. 2) и соответствующей им математической терминологией.
Рисунок 2. Схемы моделирования базовых форм оригами с комментариями
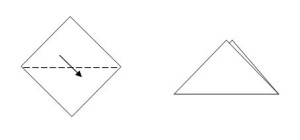
Базовая форма “Треугольник”
Комментарий: расположите квадратный лист бумаги в виде ромба и сложите его по одной из диагоналей, сгиб “долиной”.
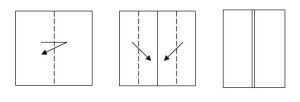
Базовая форма “Прямоугольник”
Комментарий: в исходном квадрате наметьте вертикальную среднюю линию, сгиб “долиной”. Получившиеся равные прямоугольники сложите по их средним линиям к средней линии исходного квадрата, сгибы “долиной”.
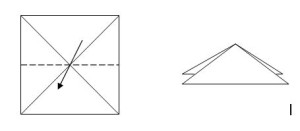
Базовая форма “Двойной треугольник”
Комментарий: в исходном квадрате наметьте диагонали, сгиб “горой”, и горизонтальную среднюю линию, сгиб “долиной”. Сложите исходный квадрат по намеченным линиям (левый и правый треугольники вогнутся по средним линиям, верхний и нижний треугольники совместятся на готовой модели).
Приведем пример занятия по топологическому моделированию на материале базовых форм оригами.
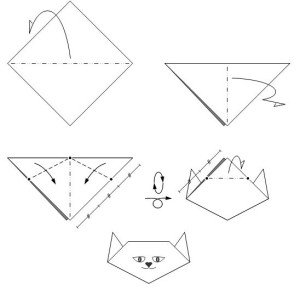
Тема занятия. Моделирование маски кошки на основе базовой формы “треугольник”.
Цель: закреплять и расширять представления детей о геометрических фигурах и их свойствах посредством базовых форм и условных обозначений оригами.
Задачи: научить детей моделировать базовую форму “треугольник” по схеме, употреблять связанную с ней математическую терминологию (рис. 2); упражнять в умении выделять элементы геометрических фигур (угол, вершина, стороны), делить фигуру на части, устанавливать пространственные отношения между ними, рассказывать о выполняемых действиях в процессе складывания; закреплять умение “читать” схему по условным знакам; совершенствовать мелкую моторику рук.
Материал: образцы готовых фигурок оригами для демонстрации, заготовки квадратных листов бумаги (по 2 на ребенка); схемы моделирования базовой формы “треугольник” (рис. 2) и маски “кошки” (рис. 3).
Ход занятия:
Воспитатель: “Ребята, сегодня я расскажу вам об оригами. Искусство оригами пришло к нам из далекой страны Японии. Оригами означает “сложенная бумага”. Не только дети, но и взрослые увлекаются оригами и придумывают новые фигурки (показ готовых масок оригами). Предлагаю вам научиться делать модели оригами. Для изготовления моделей нам потребуется квадратные или прямоугольные листы бумаги белой или цветной, цветные карандаши и коробочка, в которую будем складывать готовые маски.
А теперь мы сделаем маску кошки (показать готовый образец), помогать нам будут схемы. Чтобы сделать маску кошки, нам потребуется лист бумаги квадратной формы. Посмотрите на схему (рис. 2) и подумайте, что мы должны сделать? (Согнуть квадрат по диагонали “долиной”). Получается базовая форма “треугольник”, из нее можно складывать много разных моделей. Сделайте еще одну базовую форму “треугольник”, проверьте результат по схеме.
Посмотрите на схему (рис. 3) и определите, как мы должны расположить треугольник? (Прямым углом вниз). Что сделать дальше? (Перегибаем пополам “долиной”). Как вы это узнали? (По стрелке и прерывистой линии). На какую фигуру похожа новая фигура, почему? (Треугольник, потому что 3 стороны и 3 угла). Итак, мы наметили сгиб.
Рисунок 3. Схема моделирования маски кошки
Теперь посмотрите на схему, согнем на себя слева вниз и справа вниз два треугольника (сгиб “долиной”), доводя углы до уже намеченного сгиба. Обратите внимание: меньшая сторона отгибаемых треугольников составляет примерно треть от боковой стороны исходного треугольника. На схеме есть специальное обозначение (показать). Где левая сторона фигуры, правая? Верно! Выполните сгибы. Получились ушки кошки!
Читаем схему дальше и видим, что нужно перевернуть маску ушками вверх, затем перевернуть изделие спереди назад. Далее нужно загнуть назад один маленький треугольник сверху мордочки кошки. “Долиной” или “горой” выполняем сгиб? (“Горой”). Обратите внимание: боковая сторона отгибаемого треугольника составляет половину от боковой стороны “головы” кошки. На схеме есть специальное обозначение, кто может его показать? Прекрасно! Маска кошки готова. Нарисуйте носик и глазки! Какие красивые получились у вас маски. Хочется, чтобы вы рассказали своим мамам и папам об удивительных фигурках оригами, показали, как мы складывали маску кошки, придумали вместе с родственниками, как сделать маски собачки, лисички, бычка, лягушки, поросенка или других животных, которые вам нравятся. Попробуйте, у вас обязательно получится!
Физминутка. Все вы знаете песенку про кота Мурлыку. Давайте споем ее, демонстрируя друг другу получившиеся маски и изображая Мурлыку! Спасибо, ребята! А теперь по “волшебной тропе” (пролезть в обруч, пройти по следам, перепрыгнуть через “ручеек” и т.п.) мы доберемся до ларца, где спрятаны для каждого из вас схемы, содержащие новые обозначения оригами (рис. 1). Покажите их дома родственникам, помогите им запомнить известные вам обозначения, договорились? Тогда – в путь!”
Вторая часть серии состояла из 6 занятий с детьми подготовительных к школе групп и межгруппового мероприятия, посвященного дню космонавтики, на которых дети знакомились с информацией о планетах Солнечной системы, звездах, созвездиях. На каждом занятии создавалась модель звезды в технике модульного оригами из созвездия Большой Медведицы: каждый ребенок по словесному описанию и по схеме изготавливал один или несколько одинаковых модулей для звезды, вместе с педагогом из модулей собиралось готовое изделие (из 8 или 16 модулей) и помещалось на макет созвездия Большой Медведицы. Занятия были основаны на сюрпризных моментах, интересных сюжетах, различных играх, использовании эмоционального положительного подкрепления.
Приведем пример занятия по топологическому моделированию на материале оригами-модулей “Звездное небо”.
Тема занятия. Создание модели звезды Дубге из созвездия Большой Медведицы.
Цель: упражнять в ориентировке на листе бумаги, знакомить с приемами складывания.
Задачи: закреплять знания детей об элементах геометрических фигур, их расположении; формировать знания о приемах сгиба фигур; способствовать развитию воображения, схематического мышления.
Материал: листы квадратной формы для педагога и каждого ребенка, плакат “Созвездие Большой Медведицы”, схема складывания звезды Дубге.
Ход занятия:
Ребята, какое у нас сейчас время суток? (Утро). За утром наступит день, затем будет вечер. Вечером на небе появляются звезды. Вы любите любоваться звездами? С древних времен люди любовались звездами и объединили их в красивые созвездия, которые можно отыскать на ночном небе. Кто знает названия каких-либо созвездий? Да, самое известное созвездие – это созвездие Большой Медведицы. Оно напоминает очертание ковша, состоящее из семи ярких звезд (сосчитать изображения звезд на плакате). На нашем ковше звезды светят слабо, давайте их сделаем большими и яркими с помощью модулей оригами.
Сегодня мы сложим первую звезду – звезду Дубге. Она состоит из 8 лучей. Каждый из вас сложит по 1 лучу, и из них мы вместе склеим звезду.
Перед вами лист бумаги. Какой он формы? (Квадратной). Как еще можно назвать квадрат, почему? (Четырехугольник, у него четыре угла). Покажите верхние, нижние углы; правую, левую стороны квадрата. Молодцы!
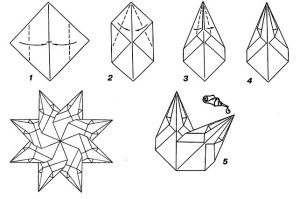
Рисунок 4. Схема моделирования звезды Дубге
Расположим квадрат так, чтобы узнавался ромб. Покажите верхний, нижний, правый, левый углы ромба. Сложим ромб по диагонали, сгиб “долиной”, левый угол соединим с правым углом (дети должны показать получившуюся диагональ, развернуть ромб). Теперь левую и правую вершину сгибаем к центру ромба (показать на схеме – рис. 4, этап 1; показать на образце).
Сосчитаем углы у получившейся фигуры, их 6. Значит, фигура называется шестиугольник. Совместим две его верхние стороны с вертикальной осью симметрии шестиугольника (диагональю исходного ромба). Так, как показано на схеме (рис. 4, этап 2). Снова получился шестиугольник, проверьте (дети пересчитывают углы). Остался последний сгиб, сделайте его самостоятельно по схеме (рис. 4, этап 3). Кто справился, у того уже получился лучик для звезды, поднимите его вверх (рис. 4, этап 4). Молодцы (проводится индивидуальная работа по исправлению неточностей, допущенных детьми при складывании).
Итак, все лучики готовы. Подходите по очереди, склеим модель звезды Дубге (рис. 4, этап 5). Посмотрите, какая она красивая (рис. 4, изображение звезды). Наша звездочка теперь светит ярко, поместим ее на наш ковш. Звезда Дубге светит в правом верхнем углу ковша.
Ребята, с каким созвездием мы сегодня познакомились? (Созвездие Большой Медведицы). На что похожа Большая Медведица? (На ковш). Сколько звезд в этом созвездии? (7). Верно! Сегодня мы собрали модель первой звезды Большой Медведицы – звезды Дубге, мы пользовались схемами и условными обозначениями. Согласны ли вы на следующем занятии продолжить увлекательное путешествие в мир звезд? Хорошо, до встречи!”
Поясним, что на следующем занятии аналогичным образом была собрана модель звезды Мерак. В ходе третьего занятия дети познакомились с самой важной для людей звездой – Солнцем, ее свойствами и значением для человека. На этом же занятии дети успешно собрали модель третьей звезды созвездия Большой Медведицы – Фегды. На четвертом занятии дети побывали в космическом путешествии на планетах Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун, Плутон. В конце занятия была собрана модель звезды Мегрец. На последующих занятиях были собраны модели звезд Алиот, Мицар и Бенетнаш, каждая из которых содержала по 16 модулей-лучей.
В качестве физминуток на занятиях применялись разминки с каштанами, например, упражнения “Колесо катится”: с некоторым давлением катать каштан между ладонями, двигая ими в противоположных направлениях; “Обезьянка хватает”: осуществить сжатие с максимальным напряжением, затем с расслаблением, не выпуская каштан из руки [3].
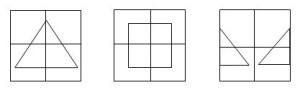
Для проведения индивидуальной работы с некоторыми детьми по закреплению представлений о геометрических фигурах, их элементах и свойствах использовались флексагоны, например, следующей раскраски:
Описание раскраски флексагона: на первой стороне флексагона изображен равносторонний треугольник, на второй – квадрат, на третьей стороне, являющейся трансформацией первой стороны и открывающейся в результате перегибания флексагона, – два равных равнобедренных треугольника, симметричные относительно вертикальной оси флексагона.
На скрытой стороне флексагона указывается:
– математический словарь раскраски: треугольник, вершина, сторона, равнобедренный треугольник, средняя линия треугольника, квадрат, прямоугольник, прямой угол, средние линии квадрата, центр квадрата, трапеция, часть, целое, равные фигуры, подобные фигуры, оси симметрии, фигуры, симметричные относительно оси, фигуры, симметричные относительно точки, биссектриса, медиана, высота;
– описывается дидактическая ситуация флексагона: на третьей стороне флексагона спрятались известные тебе фигуры. Найди и назови их (прямоугольные треугольники, трапеции). Сосчитай фигуры каждого класса. На какие предметы похожи эти фигуры? (Например: платье, колпак).
В ходе занятий были реализованы поставленные цели. Доступность бумаги как материала, простота ее обработки привлекали детей. Дошкольники начали различать такие важные детали геометрических фигур, как диагональ, средняя линия, точка пересечения диагоналей, равные фигуры и другие. С третьего занятия дети аудиально-визуальной ориентации стали употреблять названные термины в речи, к шестому занятию этого достигли и дети кинестетической ориентации. Значимую положительную динамику представлений детей о геометрических фигурах, их классах и свойствах выявила контрольная диагностика на материале “Рамки и вкладыши М. Монтессори” по сравнению с констатирующей диагностикой по этой же методике.
В результате проведенной работы было начато создание электронных баз данных для педагогов и родителей “Оригами: базовые формы и модули” и “Флексагоны: развертки, раскраски, дидактические игры”. Для родителей был оформлен уголок “Звездное небо оригами”. Им было рекомендовано закреплять знания детей на основе наблюдений созвездий, выходов в планетарий.
Проведенная опытно-экспериментальная работа показала, что топологическое моделирование на основе базовых форм и модулей оригами способствует концентрации внимания, развитию памяти, активизации мыслительных процессов.
Рассмотренные в данной статье методические материалы активно обсуждались в ходе семинаров и консультаций для методистов и воспитателей детских садов г. Смоленска и г. Магадана, следствием чего явилось расширение базы опытно-экспериментальной работы по выявлению педагогических основ математического моделирования с детьми 6-7 лет.
ЛИТЕРАТУРА
- Афонькин С.Ю. Уроки оригами в школе и дома / С.Ю. Афонькин, Е.Ю. Афонькина. – М., 1997. – 208 с.
- Нищева Н.В. Беседа “Солнце и планеты Солнечной системы” из цикла “Раз комета, два планета” / Н.В. Нищева // Дошкольная педагогика. – 2008. – № 3. – С. 26–27.
- Репина Г.А. Математическое развитие дошкольников: Современные направления / Г.А. Репина. – М. : ТЦ Сфера, 2008.
- Хлямова Т.В. Звездное небо оригами: приложение к журналу “Оригами. Искусство складывания из бумаги”. / Т.В. Хлямова. – М., 1997. – 64 с.
РЕЗЮМЕ
В статье рассматриваются педагогические основы развития навыков математического моделирования детей 6-7 лет на базе модульного оригами. Приводятся примеры занятий, способствующих развитию математических представлений дошкольников о классах и свойствах геометрических фигур.
Ключевые слова: топологическое моделирование, дети 6-7 лет.
RESUME
This article describes pedagogical fundamentals of development of skills of topological modeling based on a modular origami in a pre-school.
It also includes samples of lessons that further to development of children’s mathematical ideas about classes and properties of geometrical figures.
Keywords: topological modeling, children of 6 to 7.